
May include a brief introduction to Fermat’s Last Theorem. Usually includes most of the following topics: the Euclidean algorithm, continued fractions, Pythagorean triples, Diophantine equations such as Pell’s equation, congruences, quadratic reciprocity, binary quadratic forms, Gaussian integers, and factorization in quadratic number fields. Prerequisite: MATH 2210, MATH 2230, MATH 2940, or equivalent.Īn introductory course on number theory, the branch of algebra that studies the deeper properties of integers and their generalizations. MATH 3320 - Introduction to Number Theory

Applications from science and engineering may also be included at the instructor’s discretion.
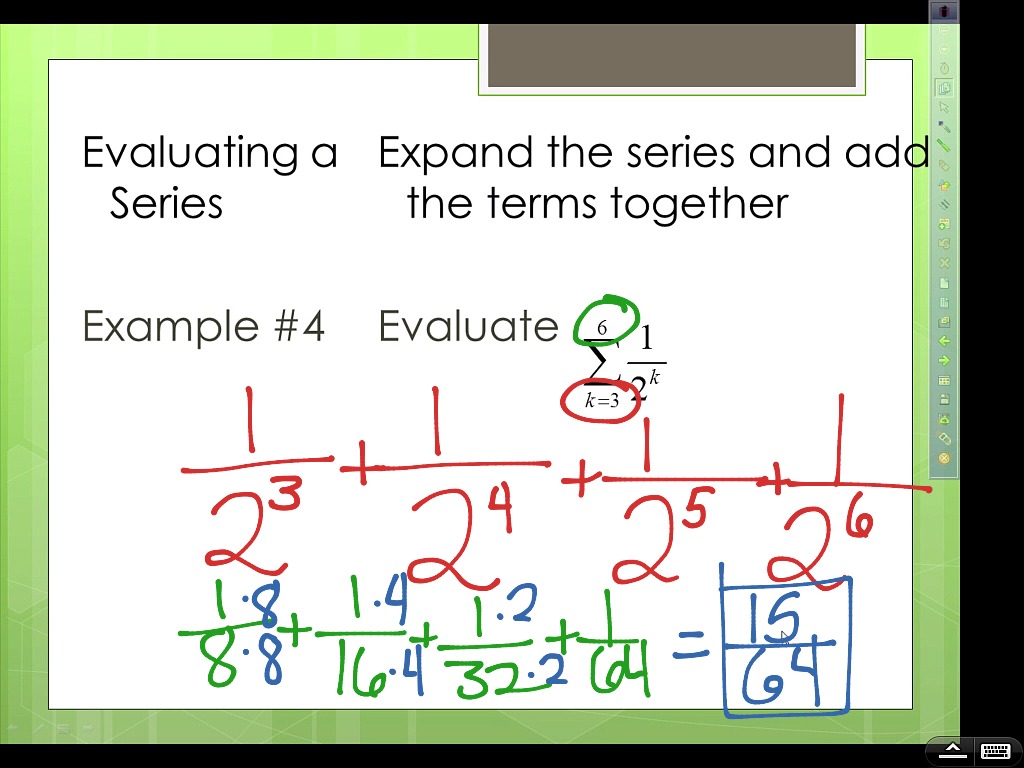
#Higher order sequences math series
Topics may include first-order and second-order differential equations, systems of linear differential equations, initial-value and two-point boundary-value problems, Sturm-Liouville theory, Sturm oscillation and comparison theory, the basic existence and uniqueness theorems, series solutions, special functions, and Laplace transforms. Student option grading.įorbidden Overlap: Due to an overlap in content, students will not receive credit for both MATH 3230 (discontinued) and MATH 3270.Ī one-semester introduction to the theory and techniques of ordinary differential equations. MATH 3270 - Introduction to Ordinary Differential Equationsįall 2023. Students who need a basic combined ODE/PDE course will find that in MATH 2930. For an upper-level treatment of ordinary differential equations, see MATH 3270. MATH 3230 - Introduction to Differential Equations Re-examines the integral theorems of vector calculus (Green, Gauss and Stokes) in the light of differential forms and applies them to problems in partial differential equations, topology, fluid mechanics and electromagnetism. The notion of a differential form encompasses such ideas as area forms and volume forms, the work exerted by a force, the flow of a fluid, and the curvature of a surface, space or hyperspace.

After a review of some relevant calculus, this course investigates manifolds and the structures that they are endowed with, such as tangent vectors, boundaries, orientations, and differential forms. Such a set is amenable to the methods of multivariable calculus. Student option grading.Ī manifold is a type of subset of Euclidean space that has a well-defined tangent space at every point.
MATH 3210 - Manifolds and Differential Formsįall 2023. Emphasis will be placed upon understanding and constructing mathematical proofs. Topics include rigorous treatment of fundamental concepts in calculus: including limits and convergence of sequences and series, compact sets continuity, uniform continuity and differentiability of functions. Provides a transition from calculus to real analysis. MATH 3110 - Introduction to Analysisįorbidden Overlap: Due to an overlap in content, students will not receive credit for both MATH 3110 and MATH 4130. Since cogent communication of mathematical ideas is important in the presentation of proofs, the course emphasizes clear, concise exposition. In this course, students learn various methods of mathematical proof, starting with basic techniques in propositional and predicate calculus and in set theory and combinatorics, and then moving to applications and illustrations of these via topics in one or more of the three main pillars of mathematics: algebra, analysis, and geometry. In mathematics the methodology of proof provides a central tool for confirming the validity of mathematical assertions, functioning much as the experimental method does in the physical sciences. This course is useful for all students who wish to improve their skills in mathematical proof and exposition, or who intend to study more advanced topics in mathematics. Prerequisite: MATH 2210, MATH 2230, MATH 2940, or equivalent. However, the study provides new evidence that multiple mechanisms may underpin the learning of FOC and HOC sequences.Please consult Is There Life After Calculus? for assistance in selecting an appropriate course. The SLI group's difficulty learning the FOC sequence is consistent with the procedural deficit hypothesis. The control group learned both sequences (FOC η p² =. Results showed that the SLI group learned the HOC sequence (η p² =. On 1 version, the sequence to be implicitly learnt comprised a FOC sequence and on the other a HOC sequence.

#Higher order sequences math serial
Twenty-five children with SLI and 27 age-matched, nonlanguage-impaired children completed 2 serial reaction time tasks. This study investigated whether implicit sequence learning problems in SLI are present for first-order conditional (FOC) and higher order conditional (HOC) sequences. A core claim of the procedural deficit hypothesis of specific language impairment (SLI) is that the disorder is associated with poor implicit sequence learning.


 0 kommentar(er)
0 kommentar(er)
